<통기타(통계 기초 타파)> #0. 변수, 가설검정, 오류, 검정력, 정규성
들어가며..
개인적인 일로 인하여 블로그에 신경을 못썼다.
군의관 생활의 절반을 지나가는 이 시점에서, 나중에 원활히 논문을 쓸 수 있기 위해 매일 뒤돌아서면 잊어버리는 통계공부를 하기 위해 책들을 구입하였고, 동시에 파이썬에도 많은 패키지가 제공되어 편리하게 통계를 돌릴 수 있지만 그래도 연구자들이 많이 사용하는 R에 대해서도 공부해보기로 하였다.
글 제목이 매우 아재느낌이 난다.
하지만 나중에 찾아보려면 약간의 오글거림과 기억에 잘 나는 제목이 필요하므로 강행하였다.


통계에 대해 다시 되짚는 시간인 만큼, 기초 용어부터 확실하게 정리하고 헷갈리는 부분 없이! 넘어가보도록 하자.
변수
연구할 때 다루는 데이터들은 모두 연구에서의 '변수'가 된다.
이 변수들이 어떤 성격을 가지고 있는지에 따라 사용 가능한 통계 기법이 달라지기 때문에 변수의 종류에 대해 파악하는 것이 매우 중요하다.
이산형 변수(discrete) = 범주형 변수(categorical)
- 명목변수 (nominal)
- 순위변수 (ordinal)
연속형 변수(continuous)
- 간격변수 (interval)
- 비율변수 (ratio)
매번 이렇게 써놓고 나면 쉽지만, 뒤돌아서면 헷갈리기 때문에 쉽게 구분하는 방법을 다시 한 번 정리하자.
변수가 취할 수 있는 값의 수를 셀 수 있다면 -> 이산형 변수
- 변수 간 우열이 없다면 명목변수, 있다면 순위변수
변수가 취할 수 있는 값이 무한하다면 -> 연속형 변수
- 더하기 빼기는 가능하지만 곱하기 나누기는 안되고, 0이 실제 zero의 의미가 없으면 간격변수 (온도 등)
- 가감승제가 모두 가능하고, 0이 zero의 의미를 가지면 비율변수 (키, 몸무게, 시간 등)
신뢰구간, 오류, 가설
이 또한 매번 헷갈리는 부분이다.
책에 나온 예를 들어 천천히 이해해보도록 하자.
동전을 던졌을 때 앞면 혹은 뒷면이 나올 확률은 각각 50%이다.
자, 내가 어떤 동전을 발견하고 이 동전을 던졌는데 앞면이 8번 뒷면이 2번 나왔다.
그렇다면 이 동전은 정상적인 동전일까?

위 그래프에서 처럼 동전을 10번 던졌을 때 앞면이 8번 나올 확률은 4.39%이다.
즉 이 동전이 정상이냐! 이상하냐!를 따지는 기준을 어디에 두냐에 따라 이 동전을 정상이라고 판단할 수도, 아니면 어딘가 이상한 동전이라고 판단할 수도 있는 것이다.
이 기준을 유의수준(level of significance) 이라고 한다.
일반적으로 5%를 많이 사용하므로 위의 경우에 대입해보면 다음과 같다.
자, 우리는 미지의 동전을 가지고 있다.
이 동전이 특이한 동전이라는 것을 판단하고 싶다면 어떻게 해야 할까?
우리는 특이한 동전이 뭔지에 대한 기준을 모르기 때문에,
일단 이 동전이 정상적인 동전이라고 가정하고 = H0, 귀무가설
이 것이 틀림을 증명하면 된다. = 귀무가설 기각
1) 정상적인 동전이라고 가정하였다. (H0)
2) 정상적인 동전이라면 "10번 던졌을 때 앞면이 나오는 횟수"라는 이산변수가 위와 같은 확률 분포를 가진다.
3) 우리의 실험에서 앞면이 8번 나왔으며, 이런 확률은 4.39%이며, 우리의 유의수준 보다 낮다.
4) "말이 안 되는" 결과가 나왔으므로 우리의 가설은 틀렸다. 귀무가설이 기각되었다.
5) 즉 대립가설을 택한다."이 미지의 동전은 뭔가 특이한 동전이다."
!!!여기서 또한 매우 중요한 개념은!!!
귀무가설은 그냥 증명하려는 가설을 부정하는 개념이 아니라!
우리가 분포를 알 수 있는 가설이라는 점이다.
위의 상황에서 실제로 이 동전이 정상적인 동전일 가능성은 4.39%이다.
이러한 오류를 1종 오류(Type 1 error, α)라고 하며, 이는 유의수준과 같다.
반대로, 이게 특수 동전이 맞는데도 일반 동전이라고 하는 것을 2종 오류(Type 2 error, β) 라고 하는데, 특수 동전일 경우에는 상황마다 확률이 다를 테니 알 수가 없다.
이제 개념에 대해 대략 알았으니, 조금 더 우리가 연구에서 마주치는 상황을 가정하여 개념을 복습해보자.
A라는 수술법이 있고, B라는 새로운 수술법이 나왔다.
A와 B를 비교하여 B가 더 좋은 수술법이라고 증명하고 싶다. 어떻게 해야 할까?
200명을 모아서 100명은 A 수술을 시행하여 결과가 평균 32점이 나왔고, 100명은 B 수술을 시행하여 결과가 평균 34점이 나왔다.
B는 미지의 수술법이므로 얼마나 좋은지 알 수가 없으므로, 마찬가지로 귀무가설을 이용하여 증명해아 한다.
H0 : B 수술은 A 수술과 결과에 차이가 없다.
H1 : B 수술은 A 수술보다 우수하다 or 결과에 차이가 없다.

H0를 주장하므로, 왼쪽의 분포 그래프는 A 수술의 분포와 같다.
즉 B 수술법은 정상적으로라면 왼쪽 그래프의 확률 분포를 따라야 한다.
이 때 우리가 연구 전 정한 유의수준 α 에 따라 임계치가 정해지고
연구 결과값인 평균 34점이 임계치를 넘어가서, p value가 유의 수준 이하라면 H0는 기각된다.
즉, 1종 오류 α는 귀무가설이 참인데 기각할 확률과 같은 의미이다.
여기서 2종 오류 β는 대립가설이 참인데 기각될 확률과 같은 의미가 되겠다.
검정력 1-β는 대립가설을 증명할 확률이 되겠다.
추가적으로
평균과 분산에 따라 분포 그래프가 달라지므로
평균의 차이가 크고 (= 두 봉우리가 멀고)
분산이 작을수록 (= 두 산이 뾰족할수록)
차이를 보기에 좋은데, 이러한 개념은 샘플 수 계산에 중요하다.
상대위험도, 오즈비
이 또한 항상 헷갈리는 내용이다.
헷갈리지 않으려면 이 개념이 어디에서 나왔는지 알아야 한다.
상대위험도
전향적 코호트 연구에서 사용
현실적으로 이런 연구가 어렵기 때문에 자주 보기 어렵다.
즉, 흡연자 100명 비흡연자 100명 잡아두고 관찰하여 폐암 발생률을 비교하는 개념이다.

흡연자에서 폐암 위험도는 90/100
비흡연자에서 폐암 위험도는 20/100
즉 상대위험도(RR)은 4.5가 된다.
오즈비
상대적으로 연구가 쉬운 단면적 연구(cross-sectional study)에서 나온 개념이므로 상대적으로 자주 보이며, RR로 근사하려는 시도가 생긴 것이다.
어느 시점에 딱 잘라서 폐암 있는 사람과 없는 사람들을 조사하였다.

odds란, 특정 군에서 질병군/비질병군의 비율을 뜻한다.
즉 위의 경우 흡연이라는 인자의 odds ratio는
(P1 / 1-P1) / (P2 / 1-P2) = P1(1-P2) / P2(1-P1) 이 되므로 이를 교차비라고도 하며
=RR * (1-P2) / (1-P1)이 되므로
P1, P2가 아주 작은 희귀한 질환일 수록 OR과 RR은 비슷해지게 된다.
정규성 검정
다시한번 변수의 종류를 나타내는 용어를 정리하자.
연속형 변수 - 비율변수, 간격변수
범주형 변수(이산) - 서열(ordinal)변수, 명목(nominal)변수
우리는 결과를 가지고 분석을 해야 하므로, 결과변수 = 종속변수의 형태에 따라 다른 통계기법을 사용해야 하며,
일반적인 느낌은 다음과 같다.
수학적이고 깔끔하네? = 결과가 정규성을 갖는 연속변수네 => A method
문과느낌 나네? = 결과가 명목변수네 => C method
이도 저도 아니네? = 결과가 정규성이 없는 연속변수이거나, 서열(순위)변수네 => B method
연속변수인지, 서열변수인지 명목변수인지는 보면 알 수 있으므로
우리에게 중요한 것은 연속변수일 때 정규성을 갖는지 판단하는 것이며, 여기에는 매우 다양한 방법들이 있다.
크게 통계적 방법을 이용한 정규성 확인과
그래프를 이용한 시각적 확인이 있으며 이 두가지는 모두 중요하다.
통계적 방법으로는 대표적으로 Shapiro-Wilk test가 있으며, R을 이용하여 검정을 진행해보자.
책에서 제공하는 data를 이용하여 진행한다.
meanData <- read.csv('./ch04_01.csv', header=TRUE)
View(meanData)
위와 같은 3개의 독립변수, 1개의 종속변수를 갖는 41개의 데이터를 불러왔고, 결과변수인 score가 정규성을 갖는지 확인해보자.
통계적 방법 : Shapiro-Wilk test
우리가 확인하고 싶은 것은 이 표본이 정규성을 띈다는 것이다.
위에서 알아보았듯 귀무가설은 우리가 확률분포를 알 수 있는 경우로 설정해야 하므로,
H0 : 표본은 정규분포를 이룬다.
H1 : 표본은 정규분포를 이루지 않는다.
라고 설정해야 한다.
따라서 보통 정규성 검정의 경우 p > 0.05여야 정규성을 받아들이는 것이다.
자세한 검정 자체는 컴퓨터가 해주므로 다 알 필요는 없을 것 같고,
대략적으로 Shapiro-Wilk test는 오차항이 정규분포를 따르는지 알아보는 검정이라고 알고 넘어가자.
따라서 R의 lm 함수를 이용하여 회귀모델을 만들고, 이 모델에서의 값들의 잔차를 이용하여 검정을 시행한다.
output = lm(score~group, data=meanData)
shapiro.test(resid(output))
p value < 0.05 이므로 귀무가설이 기각되어 정규성이 없음을 알 수 있다.
시각적 방법 : 그래프를 그려서 확인하기
정규성 검정법을은 샘플이 많아지면 많아질 수록 p 값이 낮아진다는 문제점이 있다.
그래서 샘플 수에 따라 검정법을 다르게 하기도 하는데
어쨌든 직관적으로 데이터들이 어떤 분포를 가지고 있는지 눈으로 확인하는 것이 가장 중요하겠다.
데이터의 분포를 확인할 수 있는 방법으로는
Histogram, Kernel density plot, Q-Q plot, scatter plot 등이 있다.
Histogram
hist(meanData$score)
한눈에 봐도 정규성이 없어 보인다.
이것이 그래프를 통한 정규성 확인의 장점이다.
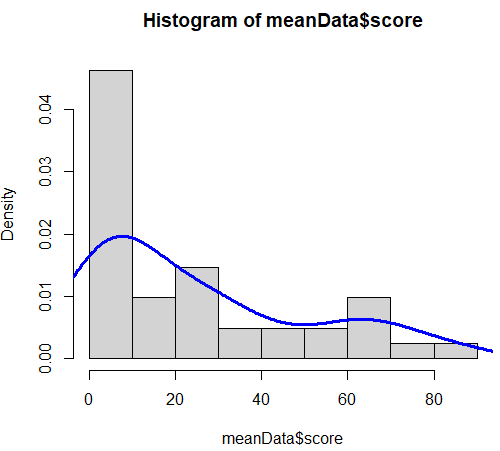
Kernel density plot
hist(meanData$score, freq=FALSE)
lines(density(meanData$score), col="blue", lwd=3)R의 histogram의 경우 y 축을 frequency로 그리기 때문에, freq=FALSE 옵션을 사용한다.
Q-Q plot
Q-Q plot은 Quantile - Quantile plot의 약자로,
표준정규분포의 분위수와 이에 대응하는 분포의 분위수를 x, y 좌표평면에 plotting 하는 개념이다.
즉 정규분포라면 직선을 띌 것이다.
qqnorm 함수는 주어진 데이터와 정규분포를 비교하는 Q-Q plot을 그리며
qqline 함수는 데이터와 분포를 비교해 이론적으로 성립해야 하는 직선 관계를 그린다.
참고로 qqplot(x, y) 함수는 두 데이터 간의 Q-Q plot을 그린다.
qqnorm(meanData$score)
qqline(meanData$score)
직선에서 많이 벗어나 있는 것을 (=정규성이 없음을) 볼 수 있다.
Scatter plot
모든 분포도의 기본과도 같은 그래프로, 실험값들에 대해서 항상 그려보면 좋다고 한다.
산점도는 평면에 그려지기 때문에 독립변수 한가지와 종속변수 한가지를 택해야 하는데
R에서는 plot(x, y)로 그리게 되고,
위의 경우에는 독립변수가 3가지이기 때문에 산점도를 여러개를 그려서 확인할 수 있다.
이를 "산점도 행렬"이라고 하며, R에서는 pairs()함수로 그릴 수 있다.
pairs(meanData)
이러한 산점도에서는 이상값(outlier)를 찾아내기도 용이하다.
검정력 분석(Power analysis)
일반적으로 표본의 갯수 n이 많아지면,
중심극한정리에 따라 모집단의 분포와 관계 없이, 모평균이 μ, 모집단 표준편차가 σ일 때
표본평균의 분포는 평균 μ, 표준편차 σ/√n 인 정규분포에 가까워진다.
즉 n이 늘어날 수록 분산이 줄어들다 줄어들다 모집단의 분산과 같아진다.
다시 말해 분포 산봉우리가 점점 뾰족해진다.
즉 n을 얼마나 올려서 뾰족산으로 만들어야 두 집단을 확실히 구분할지를 파악하는 것이 검정력 분석이다.
이 때 납작산이라도 두 개가 있어야 대충 얼마나 n을 늘려야 뾰족해질지 알 수 있기 때문에
선행연구나 pilot study를 통해 이를 파악하는 것이 중요하다.
예를 들어 pilot study나 선행연구에서 두 집단의 그래프가 핑크색과 파란색으로 나왔다.

이때 파란색 그래프는 너무 뭉툭하므로 핑크색 그래프와 구분하기가 어렵다.
즉 n수를 늘려가며 분산을 줄여야 어느정도 유의수준에서 기각이 가능할 것으로 예상되므로 이렇게 n수가 어느정도 필요할지 예측하는 것이다.
검정력 - 흔히 하는 실수
흔한 실수 중 하나가 검정력을 미리 파악하지 않고 "p=0.12가 나왔으므로 0.05보다 커서 두 군에는 차이가 없다." 라고 주장하는 것이다.
샘플 수가 충분히 커진다면 차이가 생길지 어떻게 아는가?
즉, 지금까지 연구한 것(사전연구, pilot study 등)을 통해 최소 요구하는 샘플 수를 구한 후
이 보다 많은 숫자를 연구하였음에도 두 군이 차이가 나지 않는다는 것을 보여주어야 한다.
이를 구하는 방법으로는
G*power3이라는 프로그램이나, 웹에서 sample size calculator 등을 이용하는 방법이 있다.
'Career > 의학 통계' 카테고리의 다른 글
| <통기타> #5. 진단법과 관련된 통계와 재현성 검사 (0) | 2022.12.03 |
|---|---|
| <통기타> #4. 생존분석 (0) | 2022.12.01 |
| <통기타> #3. 하나의 그룹 내의 여러 요인의 비교 - 상관 분석, 회귀 분석 (0) | 2022.11.30 |
| <통기타> #2. 짝을 이룬 자료의 비교 (0) | 2022.11.29 |
| <통기타> #1. 동질 집단 사이의 비교 (0) | 2022.11.21 |








